एनसीईआरटी Solution: कक्षा 12 रसायन विज्ञान अध्याय 1 – विलयन

1. ठोस विलयन (Solid Solution)
परिभाषा: जिस विलयन में विलेय और विलायक दोनों ठोस अवस्था में हों।
उदाहरण: पीतल (जस्ता + तांबा)

2. द्रव विलयन (Liquid Solution)
परिभाषा: जिस विलयन में विलायक द्रव अवस्था में हो।
उदाहरण: जल में नमक, जल में चीनी

3. गैसीय विलयन (Gaseous Solution)
परिभाषा: जिस विलयन में विलायक गैस अवस्था में हो।
उदाहरण: वायु (नाइट्रोजन में ऑक्सीजन, CO₂ आदि)

अवस्था के आधार पर विलयन के कुछ सामान्य उदाहरण:

विलेय	विलायक	विलयन का उदाहरण
ठोस	द्रव	नमक + जल
द्रव	द्रव	अल्कोहल + जल
गैस	द्रव	CO₂ + जल (सोडा जल)
गैस	गैस	वायु

समझने के लिए:
कुछ धातुओं में गैसें अपने कणों के बीच की खाली जगह (Interstitial space) में समा जाती हैं। ऐसी स्थिति में बनने वाला विलयन ठोस विलयन कहलाता है।

इस उदाहरण में:
विलेय = हाइड्रोजन गैस (H₂)
विलायक = पैलेडियम धातु (Pd)
अवस्था = ठोस विलयन

हाइड्रोजन गैस पैलेडियम की जाली संरचना में प्रवेश कर जाती है और एक समांगी ठोस विलयन बनता है।

(i) मोल अंश (Mole Fraction)
परिभाषा: किसी विलयन में किसी घटक के मोलों की संख्या और विलयन में उपस्थित कुल मोलों की संख्या के अनुपात को मोल अंश कहते हैं।

सूत्र:
मोल अंश = घटक के मोल / कुल मोल

(ii) मोललता (Molality)
परिभाषा: विलायक के 1 किलोग्राम में घुले विलेय के मोलों की संख्या को मोललता कहते हैं।

सूत्र:
मोललता = विलेय के मोल / विलायक का द्रव्यमान (kg में)

(iii) मोलरता (Molarity)
परिभाषा: विलयन के 1 लीटर में उपस्थित विलेय के मोलों की संख्या को मोलरता कहते हैं।

सूत्र:
मोलरता = विलेय के मोल / विलयन का आयतन (लीटर में)

(iv) द्रव्यमान प्रतिशत (Mass Percentage)
परिभाषा: विलयन के कुल द्रव्यमान में उपस्थित विलेय के द्रव्यमान का प्रतिशत द्रव्यमान प्रतिशत कहलाता है।

सूत्र:
द्रव्यमान प्रतिशत = विलेय का द्रव्यमान / विलयन का कुल द्रव्यमान × 100

दिया गया:
नाइट्रिक अम्ल का द्रव्यमान प्रतिशत = 68% (w/w)
विलयन का घनत्व = 1.504 g mL⁻¹
HNO₃ का मोलर द्रव्यमान = 63 g mol⁻¹

Step 1: 68% (w/w) का अर्थ
68% (w/w) का अर्थ है कि 100 g विलयन में:
नाइट्रिक अम्ल (HNO₃) = 68 g
जल = 32 g

Step 2: नाइट्रिक अम्ल के मोल
सूत्र:
मोल = विलेय का द्रव्यमान / मोलर द्रव्यमान

HNO₃ के मोल = 68 g / 63 g mol⁻¹ = 1.08 mol

Step 3: 100 g विलयन का आयतन
हम जानते हैं कि:
घनत्व = द्रव्यमान / आयतन

आयतन = द्रव्यमान / घनत्व = 100 g / 1.504 g mL⁻¹ = 66.5 mL

लीटर में आयतन = 0.0665 L

Step 4: मोलरता की गणना
सूत्र:
मोलरता = विलेय के मोल / विलयन का आयतन (लीटर में)

M = 1.08 mol / 0.0665 L = 16.2 mol L⁻¹

दिया गया:
ग्लूकोज विलयन = 10% (w/w)
विलयन का घनत्व = 1.2 g mL⁻¹
ग्लूकोज का मोलर द्रव्यमान = 180 g mol⁻¹
जल का मोलर द्रव्यमान = 18 g mol⁻¹

Step 1: 10% (w/w) का अर्थ
10% (w/w) का अर्थ है कि 100 g विलयन में:
• ग्लूकोज = 10 g
• जल = 90 g

जल का द्रव्यमान = 90 g
किलोग्राम में बदलने के लिए 1000 से भाग देंगे:
= 0.090 kg

Step 2: मोललता की गणना
मोललता की गणना से पहले विलेय के मोल ज्ञात करेंगे।

ग्लूकोज के मोल = 10 g / 180 g mol⁻¹ = 0.0556 mol

अब मोललता होगी:
मोललता = ग्लूकोज के मोल / विलायक (जल) का द्रव्यमान (kg में)

= 0.0556 mol / 0.090 kg = 0.62 mol kg⁻¹

Step 3: मोल अंश की गणना
सूत्र: मोल अंश = घटक के मोल / कुल मोल

जल के मोल = जल का द्रव्यमान / जल का मोलर द्रव्यमान = 90 g / 18 g mol⁻¹ = 5 mol

कुल मोल = जल के मोल + ग्लूकोज के मोल = 5 + 0.0556 = 5.0556 mol

ग्लूकोज का मोल अंश = 0.0556 / 5.0556 = 0.012

जल का मोल अंश = 5 / 5.0556 = 0.988

Step 4: मोलरता की गणना
मोलरता ज्ञात करने के लिए पहले घनत्व से विलयन का आयतन ज्ञात करेंगे।

विलयन का घनत्व = 1.2 g mL⁻¹
अतः 100 g विलयन का आयतन:
आयतन = विलयन का द्रव्यमान / विलयन का घनत्व

= 100 g / 1.2 g mL⁻¹ = 83.3 mL

लीटर में आयतन = 0.0833 L

मोलरता = विलेय (ग्लूकोज) के मोल / विलयन का आयतन (लीटर में)

= 0.0556 mol / 0.0833 L = 0.67 mol L⁻¹

दिया गया:
पहला विलयन = 25% (w/w), द्रव्यमान = 300 g
दूसरा विलयन = 40% (w/w), द्रव्यमान = 400 g

Step 1: पहले विलयन में विलेय का द्रव्यमान
25% (w/w) का अर्थ है कि 100 g विलयन में 25 g विलेय होता है।

अतः 300 g विलयन में विलेय का द्रव्यमान:
= 25 × 300 / 100
= 75 g

Step 2: दूसरे विलयन में विलेय का द्रव्यमान
40% (w/w) का अर्थ है कि 100 g विलयन में 40 g विलेय होता है।

अतः 400 g विलयन में विलेय का द्रव्यमान:
= 40 × 400 / 100
= 160 g

Step 3: मिश्रण में कुल विलेय एवं कुल विलयन
कुल विलेय का द्रव्यमान:
= 75 g + 160 g
= 235 g

कुल विलयन का द्रव्यमान:
= 300 g + 400 g
= 700 g

Step 4: द्रव्यमान प्रतिशत की गणना
सूत्र:
द्रव्यमान प्रतिशत = विलेय का द्रव्यमान / विलयन का कुल द्रव्यमान × 100

= 235 g / 700 g × 100
= 33.57%

दिया गया:
एथिलीन ग्लाइकोल C₂H₄(OH)₂ का द्रव्यमान = 222.6 g
एथिलीन ग्लाइकोल का मोलर द्रव्यमान = 62 g mol⁻¹
जल का द्रव्यमान = 200 g = 0.200 kg
विलयन का घनत्व = 1.072 g mL⁻¹

Step 1: एथिलीन ग्लाइकोल के मोल
सूत्र: मोल = एथिलीन ग्लाइकोल का द्रव्यमान / मोलर द्रव्यमान

मोल = 222.6 g / 62 g mol⁻¹
= 3.59 mol

Step 2: मोललता की गणना
सूत्र: मोललता = विलेय (एथिलीन ग्लाइकोल) के मोल / विलायक (जल) का द्रव्यमान (kg में)

जल का द्रव्यमान = 200 g = 0.200 kg

मोललता = 3.59 mol / 0.200 kg
= 17.96 mol kg⁻¹

Step 3: विलयन का कुल द्रव्यमान
कुल द्रव्यमान = एथिलीन ग्लाइकोल का द्रव्यमान + जल का द्रव्यमान

= 222.6 g + 200 g
= 422.6 g

Step 4: विलयन का आयतन
सूत्र: आयतन = विलयन का द्रव्यमान / घनत्व

आयतन = 422.6 g / 1.072 g mL⁻¹
= 394.2 mL

लीटर में आयतन = 0.3942 L

Step 5: मोलरता की गणना
सूत्र: मोलरता = विलेय (एथिलीन ग्लाइकोल) के मोल / विलयन का आयतन (लीटर में)

मोलरता = 3.59 mol / 0.3942 L
= 10.58 mol L⁻¹

दिया गया:
क्लोरोफॉर्म की मात्रा = 15 ppm (द्रव्यमान में)

इसका अर्थ है कि 10⁶ g जल में CHCl₃ = 15 g

अथवा 1 kg जल में CHCl₃ = 15 mg = 0.015 g

CHCl₃ का मोलर द्रव्यमान:
= 12 + 1 + (35.5 × 3)
= 119.5 g mol⁻¹

(i) Step 1: ppm को द्रव्यमान प्रतिशत में बदलना
सिद्धांत:
ppm का अर्थ है 10⁶ भागों में विलेय के भाग।

अर्थात 15 ppm का अर्थ है कि 10⁶ भागों वाले विलयन में विलेय के 15 भाग उपस्थित हैं।

अब हम आसानी से द्रव्यमान प्रतिशत ज्ञात कर सकते हैं:

द्रव्यमान प्रतिशत = (विलेय के भाग / विलयन के भाग) × 100

= 15 / 10⁶ × 100
= 0.0015%

(ii) Step 2: क्लोरोफॉर्म के मोल
सूत्र: मोल = विलेय का द्रव्यमान / मोलर द्रव्यमान

CHCl₃ के मोल = 0.015 g / 119.5 g mol⁻¹
= 1.26 × 10⁻⁴ mol

Step 3: मोललता की गणना
सूत्र (हिंदी में):
मोललता = विलेय के मोल / विलायक का द्रव्यमान (kg में)

यहाँ जल का द्रव्यमान = 1 kg

मोललता = (1.26 × 10⁻⁴ mol) / 1 kg
= 1.26 × 10⁻⁴ mol kg⁻¹

• जल के अणुओं के बीच H₂O–H₂O हाइड्रोजन बंध उपस्थित होते हैं।
• ऐल्कोहॉल के अणुओं के बीच ऐल्कोहॉल–ऐल्कोहॉल हाइड्रोजन बंध होते हैं।
• जब ऐल्कोहॉल और जल को मिलाया जाता है, तब ऐल्कोहॉल–जल के बीच नए हाइड्रोजन बंध बनते हैं।

• ये नए बने बंध:
– पहले से मौजूद H₂O–H₂O बंधों की तुलना में, तथा
– ऐल्कोहॉल–ऐल्कोहॉल बंधों की तुलना में कमज़ोर होते हैं।

• कमजोर अंतराआणविक बलों के कारण:
– ये अणु आसानी से वाष्प अवस्था में परिवर्तित हो जाते हैं,
– जिससे वाष्प दाब बढ़ जाता है तथा क्वथनांक कम हो जाता है।

• परिणामस्वरूप यह विलयन राउल्ट के नियम से धनात्मक विचलन प्रदर्शित करता है।

Step 1: गैस का द्रव में घुलना
• जब कोई गैस किसी द्रव में घुलती है, तो गैस के अणु द्रव के अणुओं के साथ अंतराआणविक आकर्षण बल बनाते हैं।
• इस प्रक्रिया में सामान्यतः ऊष्मा का उत्सर्जन होता है।
• अतः गैस का द्रव में घुलना एक ऊष्माक्षेपी प्रक्रिया कहलाती है।

Step 2: ताप बढ़ाने का प्रभाव
• ताप बढ़ाने पर विलयन को अतिरिक्त ऊष्मा मिलती है।
• ऊष्माक्षेपी प्रक्रिया में ताप बढ़ाने से संतुलन बाईं ओर खिसक जाता है।
• इसका अर्थ है कि द्रव में घुली गैस पुनः गैसीय अवस्था में जाने लगती है।

Step 3: विलेयता में कमी का कारण
• ताप बढ़ने से गैस के अणुओं की गतिज ऊर्जा बढ़ जाती है।
• बढ़ी हुई ऊर्जा के कारण गैस के अणु:
– द्रव में टिक नहीं पाते, तथा
– द्रव से बाहर निकल जाते हैं।
• इसलिए ताप बढ़ाने पर गैसों की द्रवों में विलेयता घट जाती है।

हेनरी का नियम:
• सर्वप्रथम हेनरी ने गैस की द्रव में विलेयता और दाब के बीच मात्रात्मक संबंध प्रस्तुत किया।
• इस नियम के अनुसार:
स्थिर ताप पर, किसी विलायक के प्रति इकाई आयतन में घुली गैस का द्रव्यमान, विलयन के संपर्क में स्थित गैस के दाब के समानुपाती होता है।

मोल अंश के रूप में नियम:
यदि विलयन में घुली गैस की विलेयता को मोल अंश (X) से व्यक्त किया जाए, तो—

किसी गैस का वाष्प अवस्था में आंशिक दाब (p), विलयन में उस गैस के मोल अंश (X) के समानुपाती होता है।

अर्थात्,
p ∝ X
या
p = K^H × X

जहाँ,
K^H = हेनरी स्थिरांक

• जब एक से अधिक गैसों का मिश्रण किसी द्रव के संपर्क में होता है, तो प्रत्येक गैस अपने-अपने आंशिक दाब के अनुसार द्रव में घुलती है।
• इसलिए हेनरी का नियम प्रत्येक गैस पर स्वतंत्र रूप से लागू होता है।

हेनरी के नियम के महत्वपूर्ण अनुप्रयोग:

(1) सोडा जल एवं शीतल पेय
• सोडा जल और शीतल पेयों में CO₂ की विलेयता बढ़ाने के लिए बोतलों को अधिक दाब पर बंद किया जाता है।
• अधिक दाब → अधिक CO₂ घुली हुई

(2) गोताखोरों में बेंड्स रोग (Bends)
• गहरे समुद्र में अधिक बाहरी दाब के कारण गोताखोरों के रक्त में नाइट्रोजन की विलेयता बढ़ जाती है।
• जब गोताखोर तेजी से सतह की ओर आते हैं, तो बाहरी दाब अचानक कम हो जाता है, जिससे घुली हुई नाइट्रोजन बुलबुलों के रूप में बाहर निकल आती है।
• ये बुलबुले रक्त नलिकाओं में रुकावट उत्पन्न करते हैं, जिससे एक खतरनाक स्थिति उत्पन्न होती है, जिसे बेंड्स (Bends) कहते हैं।
• यह एक अत्यधिक पीड़ादायक एवं जानलेवा स्थिति हो सकती है।
• इससे बचने के लिए गोताखोरों के सिलेंडरों में हीलियम मिलाकर वायु भरी जाती है।

• इस मिश्रण की संरचना इस प्रकार होती है:
11.7% हीलियम, 56.2% नाइट्रोजन तथा 32.1% ऑक्सीजन

(3) अधिक ऊँचाई पर एनॉक्सिया (Anoxia)
• अधिक ऊँचाई वाले स्थानों पर ऑक्सीजन का आंशिक दाब कम होता है।
• इसके कारण रक्त और ऊतकों में ऑक्सीजन की विलेयता कम हो जाती है।
• परिणामस्वरूप व्यक्ति को:
– चक्कर आना
– कमजोरी
– स्पष्ट सोच में कठिनाई होती है।
• इस स्थिति को एनॉक्सिया कहते हैं।

दिया गया:
एथेन का द्रव्यमान (m₁) = 6.56 × 10⁻³ g
आंशिक दाब (P₁) = 1 bar
एथेन का द्रव्यमान (m₂) = 5.00 × 10⁻² g
आंशिक दाब (P₂) = ?

Step 1: हेनरी का नियम
स्थिर ताप पर, विलयन में घुली गैस की मात्रा उस गैस के आंशिक दाब के समानुपाती होती है।

अर्थात्,
आंशिक दाब ∝ गैस की मात्रा

m = K_H × P

Step 2: Unitary method का उपयोग

द्रव्यमान	आंशिक दाब
6.56 × 10−3 g	1 bar
5.00 × 10−2 g	x

अतः गुणा करके x का मान ज्ञात करेंगे:

x = (5.00 × 10⁻² g / 6.56 × 10⁻³ g) × 1 bar

= 7.62 bar

राउल्ट का नियम (संक्षेप में):
राउल्ट के नियम के अनुसार, किसी आदर्श विलयन का वाष्प दाब उसमें उपस्थित प्रत्येक घटक के मोल अंश पर निर्भर करता है।

(A) धनात्मक विचलन (Positive Deviation)
अर्थ:
जब विलयन का वास्तविक (experimental) वाष्प दाब, राउल्ट के नियम से गणना किए गए वाष्प दाब से अधिक होता है।

कारण:
• A–B अंतराआणविक आकर्षण, A–A तथा B–B आकर्षण से कमज़ोर होता है।

परिणाम:
• अणु आसानी से वाष्प अवस्था में चले जाते हैं।
• वाष्प दाब बढ़ जाता है।

मिश्रण के चिन्ह:
• आयतन में वृद्धि → ΔV > 0
• ऊष्मा का अवशोषण → ΔH > 0

उदाहरण: एथेनॉल + जल

(B) ऋणात्मक विचलन (Negative Deviation)
अर्थ:
जब विलयन का वास्तविक (experimental) वाष्प दाब, राउल्ट के नियम से अपेक्षित वाष्प दाब से कम होता है।

कारण:
• A–B अंतराआणविक आकर्षण, A–A तथा B–B आकर्षण से अधिक मज़बूत होता है।

परिणाम:
• अणु वाष्प अवस्था में जाने से रुकते हैं।
• वाष्प दाब घट जाता है।

मिश्रण के चिन्ह:
• आयतन में कमी → ΔV < 0
• ऊष्मा का उत्सर्जन → ΔH < 0

उदाहरण: एसीटोन + क्लोरोफॉर्म

दिया गया:
विलेय = अवाष्पशील
विलयन = 2% (w/w) जलीय विलयन
विलयन का वाष्प दाब (p) = 1.004 bar
विलायक (जल) का वाष्प दाब (सामान्य क्वथनांक पर) p⁰ = 1.013 bar

2% (w/w) का अर्थ:
100 g विलयन में:
• विलेय = 2 g
• जल (विलायक) = 98 g

जल का मोलर द्रव्यमान (M₁) = 18 g mol⁻¹
विलेय का मोलर द्रव्यमान = M₂ (ज्ञात करना है)

Step 1: राउल्ट के नियम का सूत्र (अवाष्पशील विलेय के लिए)
वाष्प दाब में सापेक्ष कमी = विलेय का मोल अंश

\( \frac{p^0 - p_s}{p^0} = \frac{n_1}{n_1 + n_2} \approx \frac{n_1}{n_2} \)
जहाँ
n₁ = विलेय के मोल
n₂ = विलायक (जल) के मोल

Step 2: मोल को द्रव्यमान के रूप में लिखना

\( \frac{p^0 - p_s}{p^0} = \frac{w_1 / M_2}{w_2 / M_1} \)
(क्योंकि n = w / M)

Step 3: संख्याएँ और units रखना

\( \frac{(1.013 - 1.004) bar}{1.013 \;bar} = \frac{2 g / M_2 }{98 g / 18 \text{g mol}^{-1}} \)

Step 4: समीकरण को हल करना

\( \frac{0.009 \; bar }{1.013 \; bar} = \frac{2 \; g \times 18 \;\text{g mol}^{-1}}{98 \; g \times M_2} \)

\( M_2 = \frac{2 \; g \times 18\;\text{g mol}^{-1} }{98 \;g} \times \frac{1.013 \;bar}{0.009 \; bar} \)

\( M_2 = 41.35 \; \text{g mol}^{-1}\)
\( M_2\approx 40 \; \text{g mol}^{-1} \)

दिया गया
हेप्टेन का वाष्प दाब, p_hep^° = 105.2 kPa
हेप्टेन का द्रव्यमान = 26.0 g
हेप्टेन का मोलर द्रव्यमान = 100 g mol⁻¹

ऑक्टेन का वाष्प दाब, p_oct^° = 46.8 kPa
ऑक्टेन का द्रव्यमान = 35.0 g
ऑक्टेन का मोलर द्रव्यमान = 114 g mol⁻¹

Step 1: राउल्ट के नियम का सूत्र (इस तरीके से)
सूत्र: कुल वाष्प दाब = हेप्टेन का आंशिक वाष्प दाब + ऑक्टेन का आंशिक वाष्प दाब

\( P_T = P_{\text{Heptane}} + P_{\text{Octane}} \)
\( P_T = \left(p_{\text{Heptane}}^{\circ} \times X_{\text{Heptane}}\right)\) \(+ \left(p_{\text{Octane}}^{\circ} \times X_{\text{Octane}}\right) \)
\( P = \left( p_{\text{hep}}^{\circ} \times \frac{n_{\text{heptane}}} {n_{\text{heptane}} + n_{\text{octane}}} \right)\) \(+\) \(\left( p_{\text{oct}}^{\circ} \times \frac{n_{\text{octane}}} {n_{\text{heptane}} + n_{\text{octane}}} \right) \)

Step 2: हेप्टेन तथा ऑक्टेन के मोल लिखना

\( n_{\text{hep}} = \frac{26 \text{ g}}{100 \text{ g mol}^{-1}},\) \(\quad n_{\text{oct}} = \frac{35 \text{ g}}{114 \text{ g mol}^{-1}} \)

Step 3: सीधे मान रखना

\( P = 105.2 \times \frac{26/100}{(26/100 + 35/114)}\) \(+\) \(46.8 \times \frac{35/114}{(26/100 + 35/114)} \)

Step 4: गणना

\( P = 73.08 \text{ kPa} \)

दिया गया
ताप = 300 K
शुद्ध जल का वाष्प दाब, p^° = 12.3 kPa
विलयन = 1 मोलल अवाष्पशील विलेय का विलयन

Step 1: 1 मोलल विलयन का अर्थ
1 kg जल (विलायक) में, विलेय के मोल (n_A) = 1 mol

Step 2: जल और विलेय के मोल
जल का मोलर द्रव्यमान = 18 g mol⁻¹
1 kg जल = 1000 g

अतः जल के मोल (n_B) = द्रव्यमान ÷ मोलर द्रव्यमान

\( n_B = \frac{1000}{18} \)

जल के मोल (n_B) = 55.5 mol

विलेय के मोल (n_A) = 1 mol

कुल मोल = n_A + n_B = (1 + 55.5) mol

Step 3: विलेय का मोल अंश निकालना
सूत्र: मोल अंश = घटक के मोल / कुल मोल

\( x_A = \frac{1}{1 + 55.5} \)

\( x_A = 0.0177 \)

Step 4: राउल्ट के नियम का प्रयोग
अवाष्पशील विलेय के लिए: वाष्प दाब में सापेक्ष कमी = विलेय का मोल अंश

\( \frac{p^\circ - p_s}{p^\circ} = x_A \)

Step 5: मान रखना

\( \frac{12.3 - p_s}{12.3} = 0.0177 \)

Step 6: विलयन का वाष्प दाब निकालना

\( 12.3 - p_s = 12.3 \times 0.0177 \)

\( 12.3 - p_s = 0.218 \)

\( p_s = 12.3 - 0.218 \)

\( p_s = 12.08 \text{ kPa} \)

दिया गया
विलेय का द्रव्यमान (w_A) = ?
विलेय का मोलर द्रव्यमान (M_A) = 40 g mol⁻¹

विलायक (ऑक्टेन) का द्रव्यमान (w_B) = 114 g
विलायक (ऑक्टेन) का मोलर द्रव्यमान (M_B) = 114 g mol⁻¹

वाष्प दाब घटकर प्रारम्भिक का 80% रह जाता है
अर्थात

\( \frac{p_s}{p^\circ} = 0.80 \)

Step 1: राउल्ट के नियम का सूत्र (अवाष्पशील विलेय के लिए)
सूत्र (हिंदी में): वाष्प दाब में सापेक्ष कमी = विलेय का मोल अंश

\( \frac{p^\circ - p_s}{p^\circ} = \frac{w_A}{M_A} \times \frac{M_B}{w_B} \)

Step 2: मान रखना

\( \frac{100 - 80}{100} = \frac{w_A}{40 \; \text{g mol}^{-1}} \times \frac{114 \; \text{g mol}^{-1} }{114\; g} \)

Step 3: गणना

\( 0.20 = \frac{w_A}{40 \; g} \)

\( w_A = 8 \text{ g} \)

दिया गया

प्रथम अवस्था (I):
विलेय का द्रव्यमान (w_A) = 30 g
विलेय का मोलर द्रव्यमान = M_A (ज्ञात करना है)
जल का द्रव्यमान (w_B) = 90 g
जल का मोलर द्रव्यमान (M_B) = 18 g mol⁻¹
विलयन का वाष्प दाब (p_s1) = 2.8 kPa

द्वितीय अवस्था (II):
अतिरिक्त जल = 18 g
कुल जल = 90 + 18 = 108 g
नया वाष्प दाब (p_s2) = 2.9 kPa

शुद्ध जल का वाष्प दाब = p^° (ज्ञात करना है)

Step 1: अवाष्पशील विलेय के लिए राउल्ट का नियम
सूत्र: वाष्प दाब में सापेक्ष वृद्धि (इस रूप में प्रयुक्त)

\( \frac{p^\circ - p_s}{p_s} = \frac{w_A}{M_A} \times \frac{M_B}{w_B} \)

Step 2: प्रथम अवस्था के लिए समीकरण (I)

\( \frac{p^\circ - 2.8\; \text{kPa}}{2.8\; \text{kPa}} = \frac{30\; g}{M_A} \times \frac{18\; \text{g mol}^{-1}}{90\; g} \)

\( \frac{p^\circ - 2.8}{2.8} = \frac{6}{M_A} \) …(i)

Step 3: द्वितीय अवस्था के लिए समीकरण (II)

\( \frac{p^\circ - 2.9\; \text{kPa}}{2.9\; \text{kPa}} = \frac{30\; g}{M_A} \times \frac{18\; \text{g mol}^{-1}}{108\; g} \)

\( \frac{p^\circ - 2.9}{2.9} = \frac{5}{M_A} \) …(ii)

Step 4: समीकरण (i) और (ii) को हल करना
दोनों समीकरणों को हल करने पर प्राप्त होता है—

\( \frac{p^\circ - 2.8}{2.8} = \frac{6}{M_A} \) …(i) , \( \frac{p^\circ - 2.9}{2.9} = \frac{5}{M_A} \) …(ii)

\( p^\circ = 3.5\; \text{kPa} \)
\( M_A = 23\; \text{g mol}^{-1} \)

दिया गया
शक्कर (Sucrose) का 5% (w/w) विलयन
शक्कर विलयन का हिमांक = 271 K
शुद्ध जल का हिमांक (T_0f) = 273.15 K
ग्लूकोज का मोलर द्रव्यमान (M_Glucose) = 180 g mol⁻¹
शक्कर (सुक्रोज) का मोलर द्रव्यमान (M_Sucrose) = 342 g mol⁻¹

Step 1: शक्कर विलयन के लिए हिमांक अवनमन निकालना
सूत्र : हिमांक अवनमन = शुद्ध विलायक का हिमांक − विलयन का हिमांक

\( \Delta T_f = T^0_f - T_f \)

\( \Delta T_f = 273.15\ \text{K} - 271\ \text{K} \)

\( \Delta T_f = 2.15\ \text{K} \)

Step 2: दोनों विलयनों की सांद्रता समान है, अतः 5% (w/w) विलयन का अर्थ है, 100 g विलयन में
• विलेय, शक्कर (सुक्रोज) अथवा ग्लूकोज = 5 g
• जल (विलायक) = 95 g

Step 3: सबसे पहले हम हिमांक अवनमन के सूत्र से K_f का मान ज्ञात करते हैं।

सूत्र:

\( \Delta T_f = K_f \times m \)

\( \Delta T_f = K_f \times \frac{w_A(g)\times1000\ g}{M_A(g\ {\rm mol}^{-1}) \times w_B(g)\times1\ kg} \)

\( K_f = \frac{\Delta T_f \times M_A(g\ {\rm mol}^{-1}) \times w_B(g)\times1\ kg}{w_A(g)\times1000\ g} \)

\( K_f = \frac{2.15\ \text{K} \times 342\ \text{g mol}^{-1} \times 95\ \text{g}\times1\ \text{kg}}{5\ \text{g}\times1000\ \text{g}} \)

\( K_f \approx 14\ \text{K kg mol}^{-1} \)

Step 4: ग्लूकोज के लिए समीकरण बनाना

\( \Delta T_f = K_f \times \frac{w_A(g)\times1000\ g}{M_A(g\ {\rm mol}^{-1}) \times w_B(g)\times1\ kg} \)

\( \Delta T_f = 14\ \text{K kg mol}^{-1} \times \frac{5\ \text{g}\times1000\ \text{g}}{180\ \text{g mol}^{-1}\times95\ \text{g}\times1\ \text{kg}} \)

\( \Delta T_f = 4.1\ \text{K} \)

Step 5: ग्लूकोज विलयन का हिमांक निकालना
सूत्र : विलयन का हिमांक = शुद्ध जल का हिमांक − हिमांक अवनमन

\( \Delta T_f = T^0_f - T_f \)

\( T_f = 273.15\ \text{K} - 4.1\ \text{K} = 269.05\ \text{K} \)

दिया गया

विलेय का द्रव्यमान (w_A) = 1 g

विलायक = बेंज़ीन
विलायक का द्रव्यमान (w_B) = 20 g

AB₂ के लिए हिमांक अवनमन, ΔT_f = 2.3 K
AB₄ के लिए हिमांक अवनमन, ΔT_f = 1.3 K

बेंज़ीन के लिए
K_f = 5.1 K kg mol⁻¹

मान लें—
A का परमाण्वीय द्रव्यमान = a
B का परमाण्वीय द्रव्यमान = b

तो,
AB₂ का मोलर द्रव्यमान = a + 2b
AB₄ का मोलर द्रव्यमान = a + 4b

Step 1: हिमांक अवनमन का सूत्र
सूत्र : हिमांक अवनमन

\( \Delta T_f = K_f \times \frac{w_A(g)\times1000\ g}{M_A(g\ {\rm mol}^{-1}) \times w_B(g)\times1\ kg} \)

Step 2: AB₂ के लिए समीकरण बनाना

\( 2.3\ K = 5.1\ K\ kg\ {\rm mol}^{-1} \times \frac{1\ g \times 1000\ g}{(a+2b)\ g\ {\rm mol}^{-1} \times 20\ g \times 1\ kg} \)

a + 2b = 110.87 g mol⁻¹ …(i)

Step 3: AB₄ के लिए समीकरण बनाना

\( 1.3\ K = 5.1\ K\ kg\ {\rm mol}^{-1} \times \frac{1\ g \times 1000\ g}{(a+4b)\ g\ {\rm mol}^{-1} \times 20\ g \times 1\ kg} \)

a + 4b = 196.15 g mol⁻¹ …(ii)

Step 4: अब दोनों समीकरणों को हल करते हैं
दिए गए समीकरण:

a + 2b = 110.87 …(i)
a + 4b = 196.15 …(ii)

Step 5: (ii) − (i)

\( (a+4b)-(a+2b)=196.15-110.87 \)

\( 2b = 85.28 \)

\( b = 42.64\ g\ {\rm mol}^{-1} \)

Step 6: b का मान (i) में रखें

\( a + 2(42.64) = 110.87 \)

\( a + 85.28 = 110.87 \)

\( a = 25.59\ g\ {\rm mol}^{-1} \)

Final Answer:
A का परमाणु द्रव्यमान (a) = 25.6 g mol⁻¹
B का परमाणु द्रव्यमान (b) = 42.6 g mol⁻¹

दिया गया

ताप = 300 K (स्थिर)

प्रथम विलयन के लिए
• सांद्रता (C₁) = 36 g L⁻¹
• परासरण दाब (π₁) = 4.98 bar

द्वितीय विलयन के लिए
• परासरण दाब (π₂) = 1.52 bar
• सांद्रता (C₂) = ?

Step 1: सिद्धांत (परासरण दाब और सांद्रता का संबंध)
सिद्धांत: स्थिर ताप पर, किसी विलयन का परासरण दाब उसकी सांद्रता के समानुपाती होता है।
अर्थात

\( \pi \propto C \)

Step 2: समानुपात का सूत्र लिखना

\( \frac{\pi_1}{\pi_2} = \frac{C_1}{C_2} \)

Step 3: मान रखना (units के साथ)

\( \frac{4.98\; \text{bar}}{1.52\; \text{bar}} = \frac{36\; \text{g L}^{-1}}{C_2} \)

Step 4: सांद्रता निकालना

\( C_2 = \frac{36 \times 1.52}{4.98} \)

\( C_2 = 10.98\; \text{g L}^{-1} \)

\( \boxed{C_2 \approx 11\; \text{g L}^{-1}} \)

(i) n-हेक्सेन तथा n-ऑक्टेन
• दोनों अणु अध्रुवीय (non-polar) हैं।
• इनमें कोई स्थायी डाइपोल या आयन नहीं होता।
• इसलिए इनके बीच केवल लंदन अपसारी बल कार्य करते हैं।

(ii) I₂ तथा CCl₄
• I₂ और CCl₄ दोनों अध्रुवीय अणु हैं।
• इनके बीच भी केवल क्षणिक डाइपोल उत्पन्न होते हैं।
• अतः प्रमुख बल लंदन अपसारी बल होता है।

(iii) NaClO₄ तथा H₂O
• NaClO₄ एक आयनिक यौगिक है।
• जल एक ध्रुवीय अणु है।
• आयन और ध्रुवीय अणु के बीच आयन–डाइपोल आकर्षण बल उत्पन्न होता है।

(iv) मेथेनॉल तथा एसीटोन
• मेथेनॉल में –OH समूह उपस्थित होता है।
• एसीटोन में C=O समूह होता है।
• –OH के H और C=O के O के बीच हाइड्रोजन बंध बनता है।
• इसलिए प्रमुख आकर्षण बल हाइड्रोजन बंध है।

(v) एसीटोनाइट्राइल (CH₃CN) तथा एसीटोन (C₃H₆O)
• दोनों अणु ध्रुवीय हैं।
• लेकिन इनमें H–O या H–N जैसा समूह नहीं है।
• अतः इनके बीच डाइपोल–डाइपोल आकर्षण बल प्रमुख होता है।

n-ऑक्टेन एक अध्रुवीय (non-polar) विलायक है।
अतः इसमें वे विलेय अधिक घुलते हैं जिनकी प्रकृति भी अध्रुवीय हो या जिनमें अध्रुवीय भाग प्रमुख हो।

KCl
• KCl एक आयनिक यौगिक है।
• आयनिक यौगिक अध्रुवीय विलायकों में लगभग नहीं घुलते।
• इसलिए n-ऑक्टेन में इसकी विलेयता सबसे कम होती है।

CH₃OH (मेथेनॉल)
• मेथेनॉल एक ध्रुवीय अणु है।
• इसमें –OH समूह के कारण मजबूत अंतराआणविक आकर्षण होते हैं।
• अध्रुवीय n-ऑक्टेन में इसकी विलेयता कम होती है,
परंतु KCl से अधिक होती है।

CH₃CN (एसीटोनाइट्राइल)
• CH₃CN ध्रुवीय है, लेकिन मेथेनॉल की तुलना में कम ध्रुवीय होता है।
• इसलिए n-ऑक्टेन में इसकी विलेयता
CH₃OH से अधिक होती है।

साइक्लोहेक्सेन
• साइक्लोहेक्सेन एक अध्रुवीय हाइड्रोकार्बन है।
• “Like dissolves like” सिद्धांत के अनुसार
अध्रुवीय विलेय अध्रुवीय विलायक में आसानी से घुलता है।
• अतः n-ऑक्टेन में इसकी विलेयता सबसे अधिक होती है।

जल एक ध्रुवीय विलायक है।
जल में किसी यौगिक की विलेयता मुख्यतः इन बातों पर निर्भर करती है—
• यौगिक की ध्रुवीयता
• हाइड्रोजन बॉन्डिंग की क्षमता
• हाइड्रोकार्बन भाग का आकार

(i) फिनॉल
• फिनॉल में –OH समूह होता है, जिससे जल के साथ हाइड्रोजन बॉन्ड बनता है।
• लेकिन बेंजीन रिंग अध्रुवीय होती है।
• इसलिए फिनॉल आंशिक रूप से विलेय होता है।

(ii) टॉल्यूइन
• टॉल्यूइन एक अध्रुवीय हाइड्रोकार्बन है।
• इसमें हाइड्रोजन बॉन्डिंग की क्षमता नहीं होती।
• इसलिए यह जल में अविलेय होता है।

(iii) फॉर्मिक अम्ल
• यह एक छोटा, अत्यधिक ध्रुवीय कार्बोक्सिलिक अम्ल है।
• जल के साथ मजबूत हाइड्रोजन बॉन्ड बनाता है।
• इसलिए जल में अत्यधिक विलेय होता है।

(iv) एथिलीन ग्लाइकोल
• इसमें दो –OH समूह होते हैं।
• जल के साथ बहुत मजबूत हाइड्रोजन बॉन्डिंग होती है।
• इसलिए यह जल में अत्यधिक विलेय होता है।

(v) क्लोरोफॉर्म
• क्लोरोफॉर्म लगभग अध्रुवीय होता है।
• जल के साथ प्रभावी हाइड्रोजन बॉन्ड नहीं बनाता।
• इसलिए जल में अविलेय माना जाता है।

(vi) पेंटानॉल
• इसमें –OH समूह है, लेकिन
• लंबी हाइड्रोकार्बन श्रृंखला विलेयता कम कर देती है।
• इसलिए यह जल में आंशिक रूप से विलेय होता है।

दिया गया
जल का घनत्व = 1.25 g mL⁻¹
Na⁺ आयन का द्रव्यमान = 92 g प्रति kg जल
Na का मोलर द्रव्यमान = 23 g mol⁻¹

Step 1: Na⁺ आयन के मोल निकालना
सूत्र : मोल = द्रव्यमान / मोलर द्रव्यमान
Na⁺ के मोल = \( \frac{92\ \text{g}}{23\ \text{g mol}^{-1}} = 4\ \text{mol} \)

Step 2: विलयन का कुल द्रव्यमान निकालना
1 kg जल = 1000 g
कुल विलयन का द्रव्यमान = जल का द्रव्यमान + Na⁺ का द्रव्यमान
= 1000 g + 92 g
= 1092 g

Step 3: विलयन का आयतन निकालना
सूत्र: घनत्व = द्रव्यमान / आयतन
आयतन = द्रव्यमान / घनत्व
आयतन = \( \frac{1092\ \text{g}}{1.25\ \text{g mL}^{-1}} = 873.6\ \text{mL} \)
= 0.8736 L

Step 4: मोलरता की गणना
सूत्र: मोलरता = विलेय के मोल / विलयन का आयतन (लीटर में)
मोलरता = \( \frac{4\ \text{mol}}{0.8736\ \text{L}} = 4.58\ \text{mol L}^{-1} \)

दिया गया
CuS का विलेयता गुणनफल, Ksp = 6 × 10⁻¹⁶

Step 1: आयनीकरण समीकरण लिखना
CuS (s) ⇌ Cu²⁺ (aq) + S²⁻ (aq)
मान लेते हैं कि CuS की विलेयता = s mol L⁻¹
तब, [Cu²⁺] = s तथा [S²⁻] = s

Step 2: Ksp का व्यंजक लिखना
सूत्र: Ksp = [Cu²⁺][S²⁻]
\( K_{sp} = s \times s = s^2 \)

Step 3: मान रखना
\( 6 \times 10^{-16} = s^2 \)

Step 4: s निकालना
\( s = \sqrt{6 \times 10^{-16}} \)
\( s = 2.45 \times 10^{-8}\ \text{mol L}^{-1} \)

दिया गया
विलेय (एस्पिरिन) का द्रव्यमान = 6.5 g
विलायक (एसीटोनाइट्राइल) का द्रव्यमान = 450 g

Step 1: विलयन का कुल द्रव्यमान निकालना
सूत्र : कुल द्रव्यमान = विलेय का द्रव्यमान + विलायक का द्रव्यमान
कुल द्रव्यमान = 6.5 g + 450 g = 456.5 g

Step 2: भार प्रतिशत का सूत्र लगाना
सूत्र : भार प्रतिशत = (विलेय का द्रव्यमान / विलयन का कुल द्रव्यमान) × 100

भार प्रतिशत = \( \frac{6.5\ \text{g}}{456.5\ \text{g}} \times 100 = 1.42\% \ \text{w/w} \)

दिया गया
विलेय (नैलार्फीन) का द्रव्यमान (wA) = 1.5 mg = 0.0015 g
विलेय (नैलार्फीन) का मोलर द्रव्यमान (MA) = 311 g mol⁻¹
विलयन की मोललता (m) = 1.5 × 10⁻³ m

Step 1: मोललता का सूत्र लिखना
सूत्र : मोललता (m) = विलेय के मोल / विलायक का द्रव्यमान (kg में)

\( m=\frac{n_A\;(\mathrm{mol})}{w_B\;(\mathrm{kg})} \)

\( m=\frac{w_A\;(\mathrm{g})} {M_A\;(\mathrm{g\,mol}^{-1}) \times w_B\;(\mathrm{kg})} \)

\( m=\frac{w_A\;(\mathrm{g}) \times 1000\,\mathrm{g}} {M_A\;(\mathrm{g\,mol}^{-1}) \times w_B\;(\mathrm{g}) \times 1\,\mathrm{kg}} \)

जहाँ, m = मोललता
wB = विलायक (जल) का द्रव्यमान (g में)

Step 2: मान रखना
\( 1.5\times 10^{-3}\, m \; (\text{or mol kg}^{-1}) = \frac{0.0015\,\mathrm{g}}{311\,\mathrm{g\,mol}^{-1}} \times \frac{1000\,\mathrm{g}}{w_B\,(\mathrm{g}) \times 1\,\mathrm{kg}} \)

Step 3: wB (जल का द्रव्यमान) निकालना
\( w_B = \frac{0.0015\,\mathrm{g}}{311\,\mathrm{g\,mol}^{-1}} \times \frac{1000\,\mathrm{g}} {1.5\times 10^{-3}\,\mathrm{mol\,kg}^{-1}\times 1\,\mathrm{kg}} \)
\( w_B = 3.2154\ \text{g} \)

Step 4: विलयन का कुल द्रव्यमान निकालना
सूत्र: विलयन का द्रव्यमान = विलेय का द्रव्यमान + विलायक का द्रव्यमान
विलयन का द्रव्यमान = 0.0015 g + 3.2154 g
= 3.2169 g
≈ 3.216 g

दिया गया
विलयन की मोललता (m) = 0.15 mol kg⁻¹
विलायक = मेथेनॉल
मेथेनॉल का द्रव्यमान = 1 kg (मोललता की परिभाषा के अनुसार)
बेंज़ोइक अम्ल (C₆H₅COOH) का मोलर द्रव्यमान = 122 g mol⁻¹

Step 1: मोललता की परिभाषा लिखना
सूत्र : मोललता = विलेय के मोल / विलायक का द्रव्यमान (kg में)

Step 2: बेंज़ोइक अम्ल के मोल निकालना
मोललता = 0.15 m
विलायक = 1 kg
अतः विलेय (बेंज़ोइक अम्ल) के मोल = 0.15 mol

Step 3: बेंज़ोइक अम्ल का द्रव्यमान निकालना
सूत्र : द्रव्यमान = मोल × मोलर द्रव्यमान
द्रव्यमान = 0.15 mol x 122 g mol^-1
= 18.3 g

मुख्य सिद्धांत
हिमांक अवनमन एक अणुसंख्यक गुणधर्म है।
यह विलयन में उपस्थित कुल कणों की संख्या पर निर्भर करता है, न कि विलेय की प्रकृति पर।

Step 1: आयनीकरण का प्रभाव
• एसीटिक अम्ल (CH₃COOH) एक दूर्बलअम्ल है।
• यह जल में कम आयनीकरण करता है।
• इसलिए विलयन में कणों की संख्या कम होती है।
→ हिमांक अवनमन कम होता है।

Step 2: इलेक्ट्रॉन आकर्षी समूहों का प्रभाव
• ट्राइक्लोरोएसीटिक अम्ल (CCl₃COOH) में
तीन Cl परमाणु उपस्थित होते हैं।
• ट्राइफ्लुओरोएसीटिक अम्ल (CF₃COOH) में
तीन F परमाणु उपस्थित होते हैं।
• Cl और F दोनों इलेक्ट्रॉन आकर्षी (–I प्रभाव) दिखाते हैं।
• F का –I प्रभाव Cl से अधिक होता है।

Step 3: आयनीकरण और कणों की संख्या
• –I प्रभाव बढ़ने से → O–H बंध कमजोर होता है
→ अम्लीय क्षमता बढ़ती है
→ आयनीकरण अधिक होता है

• इसलिए
– एसीटिक अम्ल → कम आयनीकरण
– ट्राइक्लोरोएसीटिक अम्ल → अधिक आयनीकरण
– ट्राइफ्लुओरोएसीटिक अम्ल → सर्वाधिक आयनीकरण
→ विलयन में कणों की संख्या इसी क्रम में बढ़ती है।

निष्कर्ष
आयनीकरण जितना अधिक → कणों की संख्या उतनी अधिक →
हिमांक अवनमन उतना अधिक
इसलिए क्रम है: CH₃COOH < CCl₃COOH < CF₃COOH

दिया गया
विलेय = CH₃CH₂CHClCOOH
विलेय का द्रव्यमान = 10 g
विलेय का मोलर द्रव्यमान (CH₃CH₂CHClCOOH) = 122.5 g mol⁻¹

विलायक (जल) का द्रव्यमान = 250 g = 0.250 kg
Kₐ = 1.4 × 10⁻³
Kf = 1.86 K kg mol⁻¹

Step 1: विलेय के मोल निकालना
मोल = द्रव्यमान / मोलर द्रव्यमान
मोल = ¹⁰/_122.5 = 8.16 × 10⁻² mol

Step 2: विलयन की मोललता निकालना
सूत्र : मोललता = विलेय के मोल / विलायक का द्रव्यमान (kg में)
m = ^{8.16 × 10−2}/_0.250 = 0.3264 mol kg⁻¹

Step 3: आयनीकरण की डिग्री (α) निकालना
दूर्बल अम्ल के लिए:
α = √(Kₐ / C)

यहाँ, C ≈ m = 0.3264
α = √(1.4 × 10⁻³ / 0.3264) = 0.065

Step 4: van’t Hoff factor (i) निकालना
CH₃CH₂CHClCOOH ⇌ CH₃CH₂CHClCOO⁻ + H⁺
दूर्बल इलेक्ट्रोलाइट के लिए
i = 1 + α
i = 1 + 0.065 = 1.065

Step 5: हिमांक अवनमन की गणना
सूत्र :
ΔT_f = i . Kf . m
ΔT_f = 1.065 × 1.86 × 0.3264
ΔT_f = 0.649 K ≈ 0.65 K

दिया गया
👉 विलेय = CH₂FCOOH
👉 विलेय (CH₂FCOOH) का द्रव्यमान = 19.5 g
👉 विलेय (CH₂FCOOH) का मोलर द्रव्यमान = 78 g mol⁻¹
👉 विलायक (जल) का द्रव्यमान = 500 g = 0.500 kg
👉 हिमांक अवनमन, ΔT_f = 1.0 °C
👉 जल के लिए K_f = 1.86 K kg mol⁻¹

Step 1: विलेय के मोल निकालना
सूत्र: मोल = द्रव्यमान / मोलर द्रव्यमान
\( \text{मोल} = \frac{19.5\ \mathrm{g}}{78\ \mathrm{g\ mol^{-1}}} = 0.25\ \mathrm{mol} \)

Step 2: विलयन की मोललता निकालना
सूत्र : मोललता = विलेय के मोल / विलायक का द्रव्यमान (kg में)
\( m = \frac{0.25\ \mathrm{mol}}{0.500\ \mathrm{kg}} \)
\( m = 0.50\ \mathrm{mol\ kg^{-1}} \)

Step 3: वैन्ट हॉफ गुणक (i) निकालना
सूत्र:
\( \Delta T_f = i \times K_f \times m \)
\( i = \frac{\Delta T_f}{K_f \times m} \)
\( i = \frac{1.0\ \mathrm{K}}{1.86\ \mathrm{K\ kg\ mol^{-1}} \times 0.50\ \mathrm{mol\ kg^{-1}}} \)
\( i = 1.075 \)

Step 4: आयनीकरण की मात्रा (α) निकालना
\( \mathrm{CH_2FCOOH \rightleftharpoons CH_2FCOO^- + H^+} \)
यह एक मोनोप्रोटिक दूर्बल अम्ल है, अतः
\( i = 1 + \alpha \)
\( \alpha = i - 1 \)
\( \alpha = 1.075 - 1 = 0.075 \)

Step 5: वियोजन स्थिरांक (Kₐ) की गणना
सूत्र:
\( K_a = \frac{C\alpha^2}{1-\alpha} \)
यहाँ, \( C \approx m = 0.50\ \mathrm{mol\ L^{-1}} \)
\( K_a = \frac{0.50 \times (0.075)^2}{1 - 0.075} \)
\( K_a = \frac{0.0028}{0.925} \)
\( K_a = 3.1 \times 10^{-3} \)

दिया गया
👉 ताप = 293 K
👉 शुद्ध जल का वाष्प दाब, P⁰ = 17.535 mm Hg
👉 ग्लूकोज का द्रव्यमान = 25 g
👉 ग्लूकोज का मोलर द्रव्यमान = 180 g mol⁻¹
👉 जल का द्रव्यमान = 450 g
👉 जल का मोलर द्रव्यमान = 18 g mol⁻¹

Step 1: जल और ग्लूकोज के मोल निकालना
सूत्र : मोल = द्रव्यमान / मोलर द्रव्यमान

विलेय (ग्लूकोज) के मोल:
\( n_1 = \frac{25\ \mathrm{g}}{180\ \mathrm{g\ mol^{-1}}} = 0.138\ \mathrm{mol} \)

जल के मोल:
\( n_2 = \frac{450\ \mathrm{g}}{18\ \mathrm{g\ mol^{-1}}} = 25\ \mathrm{mol} \)

Step 2: राउल्ट के नियम का प्रयोग
सूत्र : वाष्प दाब में सापेक्ष कमी = विलेय का मोल अंश
\( \frac{p^\circ - p_s}{p^\circ} = \frac{n_1}{n_1 + n_2} \)

Step 3: मान रखना
\( \frac{17.535 - p_s}{17.535} = \frac{0.138}{0.138 + 25} \)

Step 4: वाष्प दाब निकालना
\( 17.535 - p_s = \frac{0.138}{25.138} \times 17.535 \)
\( 17.535 - p_s = 0.096 \)
\( p_s = 17.535 - 0.096 \)
\( p_s = 17.44\ \mathrm{mm\ Hg} \)

दिया गया
ताप = 298 K
हेनरी स्थिरांक, K_H = 4.27 × 10⁵ mm Hg
मीथेन का दाब, p = 760 mm Hg

Step 1: हेनरी के नियम का सूत्र लिखना
सूत्र : गैस का आंशिक दाब = हेनरी स्थिरांक × विलयन में गैस का मोल अंश
\( p = K_H \times x \)

Step 2: मोल अंश (x) के लिए सूत्र लिखना
\( x = \frac{p}{K_H} \)

Step 3: मान रखना (units के साथ)
\( x = \frac{760\ \mathrm{mm\ Hg}}{4.27 \times 10^5\ \mathrm{mm\ Hg}} \)

Step 4: गणना
\( x = 1.78 \times 10^{-3} \)

दिया गया
द्रव A का द्रव्यमान = 100 g
द्रव A का मोलर द्रव्यमान (M_A) = 140 g mol⁻¹

द्रव B का द्रव्यमान = 1000 g
द्रव B का मोलर द्रव्यमान (M_B) = 180 g mol⁻¹
शुद्ध द्रव B का वाष्प दाब, P_B⁰ = 500 Torr
विलयन का कुल वाष्प दाब, P_T = 475 Torr

Step 1: द्रव A और B के मोल निकालना
द्रव A के मोल
\( n_A = \frac{100\ \mathrm{g}}{140\ \mathrm{g\ mol^{-1}}} = 0.714\ \mathrm{mol} \)

द्रव B के मोल
\( n_B = \frac{1000\ \mathrm{g}}{180\ \mathrm{g\ mol^{-1}}} = 5.556\ \mathrm{mol} \)

कुल मोल = 0.714 + 5.556 = 6.270 mol

Step 2: द्रव B का मोल अंश निकालना
B का मोल अंश = B का मोल / कुल मोल
\( x_B = \frac{5.556}{6.270} = 0.886 \)

Step 3: विलयन में द्रव B का वाष्प दाब निकालना
राउल्ट का नियम:
\( p_B = x_B \times p_B^\circ \)
\( p_B = 0.886 \times 500 = 443\ \mathrm{Torr} \)

Step 4: विलयन में द्रव A का वाष्प दाब निकालना
कुल वाष्प दाब, \( P_T = p_A + p_B \)
\( p_A = P_T - p_B \)
\( p_A = 475 - 443 = 32\ \mathrm{Torr} \)

Step 5: द्रव A का मोल अंश निकालना
A का मोल अंश = A का मोल / कुल मोल
\( x_A = \frac{0.714}{6.270} = 0.114 \)

Step 6: शुद्ध द्रव A का वाष्प दाब निकालना
राउल्ट का नियम:
\( p_A = x_A \times p_A^\circ \)
\( p_A^\circ = \frac{p_A}{x_A} \)
\( p_A^\circ = \frac{32}{0.114} \)
\( p_A^\circ \approx 280\ \mathrm{Torr} \)

दिया गया
ताप = 328 K
शुद्ध एसीटोन का वाष्प दाब = 741.8 mm Hg
शुद्ध क्लोरोफॉर्म का वाष्प दाब = 632.8 mm Hg
तालिका में विभिन्न संघटनों पर प्रेक्षित वाष्प दाब दिए गए हैं।

Step 1: आदर्श विलयन के लिए राउल्ट का नियम
एसीटोन के लिए
एसीटोन का वाष्प दाब = एसीटोन का मोल अंश × शुद्ध एसीटोन का वाष्प दाब
\( p_{\text{acetone}} = x_{\text{acetone}} \times p_{\text{acetone}}^\circ \)

क्लोरोफॉर्म के लिए
क्लोरोफॉर्म का वाष्प दाब = क्लोरोफॉर्म का मोल अंश × शुद्ध क्लोरोफॉर्म का वाष्प दाब
\( p_{\text{chloroform}} = x_{\text{chloroform}} \times p_{\text{chloroform}}^\circ \)

कुल वाष्प दाब
\( P_T = p_{\text{acetone}} + p_{\text{chloroform}} \)

Step 2: ग्राफ बनाने की विधि
• X-अक्ष: एसीटोन का मोल अंश
• Y-अक्ष: वाष्प दाब (mm Hg)

एक ही ग्राफ पर तीन वक्र बनाइए—
1. एसीटोन का वाष्प दाब बनाम एसीटोन का मोल अंश
2. क्लोरोफॉर्म का वाष्प दाब बनाम एसीटोन का मोल अंश
3. कुल वाष्प दाब बनाम एसीटोन का मोल अंश

अब तालिका में दिए गए प्रेक्षित (experimental) मानों को उसी ग्राफ पर बिंदुओं के रूप में प्लॉट कीजिए।



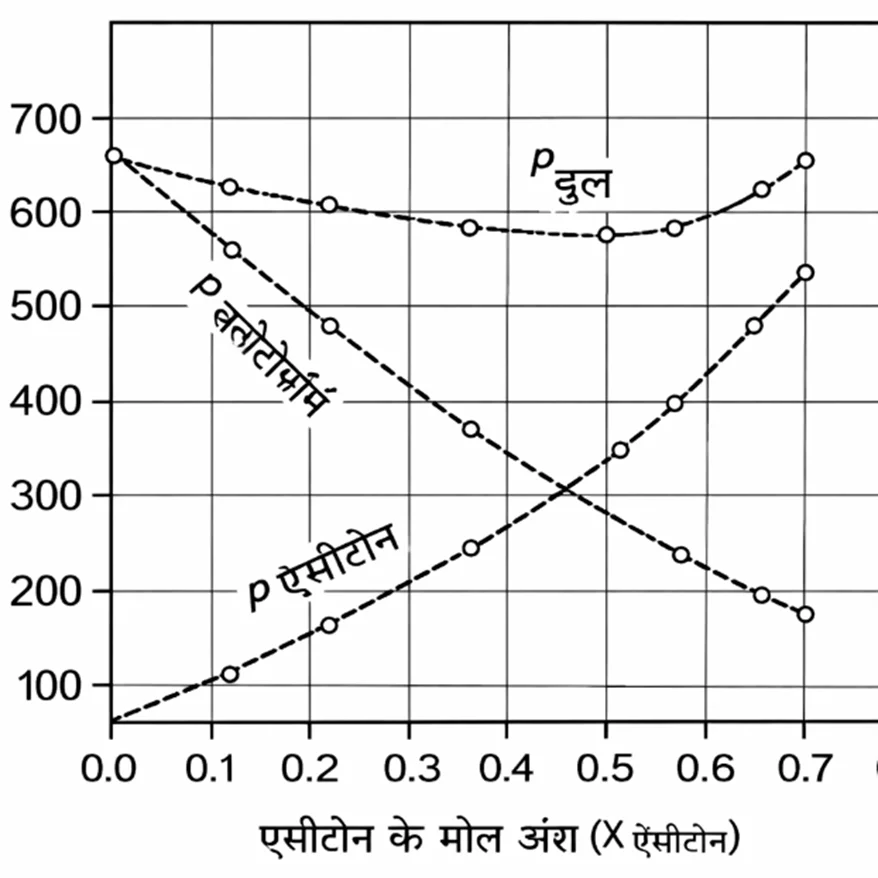
Step 3: प्रेक्षित आँकड़ों से निष्कर्ष
• प्रेक्षित कुल वाष्प दाब, राउल्ट के नियम से प्राप्त सैद्धांतिक कुल वाष्प दाब से कम है।
• अर्थात वास्तविक वक्र, आदर्श वक्र के नीचे स्थित होता है।

Step 4: विचलन का कारण
• एसीटोन और क्लोरोफॉर्म के बीच मज़बूत अंतराआणविक आकर्षण (हाइड्रोजन बॉन्डिंग) पाया जाता है।
• A–B आकर्षण, A–A तथा B–B आकर्षण से अधिक मज़बूत होता है।
• इसलिए अणु वाष्प अवस्था में जाने से रुकते हैं और वाष्प दाब घट जाता है।

निष्कर्ष
चूँकि वास्तविक वाष्प दाब आदर्श वाष्प दाब से कम है, अतः यह विलयन ऋणात्मक विचलन दर्शाता है।

दिया गया
बेंज़ीन का द्रव्यमान = 80 g
बेंज़ीन का मोलर द्रव्यमान = 78 g mol⁻¹

टॉल्यूइन का द्रव्यमान = 100 g
टॉल्यूइन का मोलर द्रव्यमान = 92 g mol⁻¹

शुद्ध बेंज़ीन का वाष्प दाब, p°(benzene) = 50.71 mm Hg
शुद्ध टॉल्यूइन का वाष्प दाब, p°(toluene) = 32.06 mm Hg

Step 1: बेंज़ीन और टॉल्यूइन के मोल निकालना
बेंज़ीन के मोल
\( n_{\mathrm{benzene}} = \frac{80\ \mathrm{g}}{78\ \mathrm{g\ mol^{-1}}} = 1.026\ \mathrm{mol} \)

टॉल्यूइन के मोल
\( n_{\mathrm{toluene}} = \frac{100\ \mathrm{g}}{92\ \mathrm{g\ mol^{-1}}} = 1.087\ \mathrm{mol} \)

कुल मोल = 1.026 + 1.087 = 2.113 mol

Step 2: द्रव अवस्था में मोल अंश निकालना
बेंज़ीन का मोल अंश (द्रव अवस्था में)
\( x_{\mathrm{benz}} = \frac{1.026}{2.113} = 0.486 \)

टॉल्यूइन का मोल अंश
\( x_{\mathrm{toluene}} = 1 - 0.486 = 0.514 \)

Step 3: राउल्ट के नियम से आंशिक वाष्प दाब निकालना
बेंज़ीन का आंशिक वाष्प दाब
\( p_{\mathrm{benz}} = x_{\mathrm{benz}} \times p_{\mathrm{benz}}^\circ \)
\( p_{\mathrm{benz}} = 0.486 \times 50.71 = 24.64\ \mathrm{mm\ Hg} \)

टॉल्यूइन का आंशिक वाष्प दाब
\( p_{\mathrm{tol}} = 0.514 \times 32.06 = 16.48\ \mathrm{mm\ Hg} \)

Step 4: कुल वाष्प दाब निकालना
\( P_T = P(\text{Benzene}) + P(\text{Toluene}) \)
\( P_T = 24.64 + 16.48 = 41.12\ \mathrm{mm\ Hg} \)

Step 5: वाष्प अवस्था में बेंज़ीन का मोल अंश
सूत्र: वाष्प अवस्था में मोल अंश = घटक का आंशिक वाष्प दाब / कुल वाष्प दाब
\( y_{\mathrm{benz}} = \frac{24.64}{41.12} = 0.60 \)

दिया गया
कुल दाब = 10 atm
वायु में ऑक्सीजन = 20%
वायु में नाइट्रोजन = 79%
हेनरी स्थिरांक (298 K पर):
K_H(O₂) = 3.30 × 10⁷ mm
K_H(N₂) = 6.51 × 10⁷ mm
1 atm = 760 mm Hg

Step 1: ऑक्सीजन और नाइट्रोजन का आंशिक दाब निकालना
सूत्र : आंशिक दाब = आयतन प्रतिशत × कुल दाब

ऑक्सीजन का आंशिक दाब
\( \frac{20}{100} \times 10 = 2\ \mathrm{atm} \)
\( P_{O_2} = 2 \times 760 = 1520\ \mathrm{mm\ Hg} \)

नाइट्रोजन का आंशिक दाब
\( \frac{79}{100} \times 10 = 7.9\ \mathrm{atm} \)
\( P_{N_2} = 7.9 \times 760 = 6004\ \mathrm{mm\ Hg} \)

Step 2: हेनरी के नियम का प्रयोग
सूत्र : \( p = K_H \times x \)
अर्थात
\( x = \frac{p}{K_H} \)

Step 3: जल में ऑक्सीजन का मोल अंश
\( x_{O_2} = \frac{P_{O_2}}{K_H} \)
\( x_{O_2} = \frac{1520}{3.30 \times 10^7} \)
\( x_{O_2} = 4.61 \times 10^{-5} \)

Step 4: जल में नाइट्रोजन का मोल अंश
\( x_{N_2} = \frac{P_{N_2}}{K_H} \)
\( x_{N_2} = \frac{6004}{6.51 \times 10^7} \)
\( x_{N_2} = 9.22 \times 10^{-5} \)

दिया गया
परासरण दाब, \( \pi \) = 0.75 atm
ताप, T = 27°C = 300 K
विलयन का आयतन, V = 2.5 L
van’t Hoff गुणक, i = 2.47
गैस नियतांक, R = 0.0821 L atm K⁻¹ mol⁻¹
CaCl₂ का मोलर द्रव्यमान = 40 + 2 × 35.5 = 111 g mol⁻¹

Step 1: परासरण दाब का सूत्र
सूत्र:
\( \pi = i \frac{n}{V} RT \)

मोल (n) के लिए—
\( n = \frac{\pi \times V}{i \times R \times T} \)

Step 2: मान रखना (units के साथ)
\( n = \frac{0.75\,\mathrm{atm} \times 2.5\,\mathrm{L}} {2.47 \times 0.0821\,\mathrm{L\,atm\,K^{-1}\,mol^{-1}} \times 300\,\mathrm{K}} \)

Step 3: CaCl₂ का मोल की गणना
\( n = \frac{1.875}{60.836} \)
\( n = 0.0308\ \mathrm{mol} \)

Step 4: CaCl₂ का द्रव्यमान निकालना
सूत्र : द्रव्यमान = CaCl₂ का मोल × CaCl₂ का मोलर द्रव्यमान
द्रव्यमान \( = 0.0308 \times 111 \)
\( = 3.42\ \mathrm{g} \)

दिया गया
K₂SO₄ का द्रव्यमान = 25 mg = 0.025 g
विलयन का आयतन = 2 L
ताप = 25°C = 298 K
K₂SO₄ का मोलर द्रव्यमान = (2 × 39) + 32 + (4 × 16) = 174 g mol⁻¹
गैस नियतांक, R = 0.0821 L atm K⁻¹ mol⁻¹

Step 1: K₂SO₄ के मोल निकालना
सूत्र : मोल = द्रव्यमान / मोलर द्रव्यमान
\( n = \frac{0.025\ \mathrm{g}}{174\ \mathrm{g\ mol^{-1}}} \)
\( n = 0.0001436\ \mathrm{mol} \)

Step 2: van’t Hoff factor (i) निकालना
K₂SO₄ पूर्णतः विघटित होता है:
\( \mathrm{K_2SO_4 \rightarrow 2K^+ + SO_4^{2-}} \)
कुल आयन = 3
अतः \( i = 3 \)

Step 3: परासरण दाब का सूत्र लगाना
सूत्र:
\( \pi = i \frac{n}{V} RT \)

Step 4: मान रखना (units के साथ)
\( \pi = 3 \times \frac{0.0001436\,\mathrm{mol}}{2\,\mathrm{L}} \times 0.0821\,\mathrm{L\,atm\,K^{-1}\,mol^{-1}} \times 298\,\mathrm{K} \)

Step 5: गणना
\( \pi = 5.2 \times 10^{-3}\ \mathrm{atm} \)